Introduction
Welcome to our blog, where we explore the details of categorical propositions, a basic concept for a number of competitive exams, including SET, SSC, CSIR NET, UGC NET, and more. It will explain the basics of the square of opposition and discuss the differences between distributed and undistributed categorical propositions. Understanding these ideas not only helps you win tests, but it also provides a strong basis for understanding more complex logic and reasoning topics. So let’s set off on this discovery and learning path together.
What are Categorical Propositions?
A categorical proposition is a that relates two classes categories. It typically consists of a subject and a predicate connected by a copula (such as “is” or “are”). For example, “All humans are mortal” is a categorical proposition that asserts a relationship between the class of humans and the class of mortals.
Types of Categorical Propositions
Four Categorical Proposition
In traditional logic, there are four standard forms of categorical propositions based on the quality (affirmative or negative) and quantity (universal or particular) of the statement. These four forms are:
- A– All S are P (Universal Affirmative)
- E– No S are P (Universal Negative)
- I– Some S are P (Particular Affirmative)
- O– Some S are not P (Particular Negative)
Distributed vs. Undistributed Categorical Proposition
A distributed categorical proposition is one that makes a claim about every member of a class, either positively or negatively. In contrast, an undistributed categorical proposition only makes a claim about some members of a class.
Square of Opposition between Propositions
The square of opposition is a diagram that represents the relationships between the four standard categorical propositions. It illustrates how each type of proposition relates to the others in terms of contradictoriness, contrariety, subcontrariety, and subalternation.
Contrary
Relationship between “All and No”
Eg : All S are P and No S is P
Sub Contrary
Relationship between Some and Some not
Eg: Some S are P and Some S are not P
Subalton
Relationship between “All and Some” and “No and Some not”
Eg: All S are P and Some S are P
No S is P and Some S is not P
Contradictory
Relationship between “All and Some not” and “No and Some”.
Eg : All S are P and Some S are not P
No S is P and Some S are P
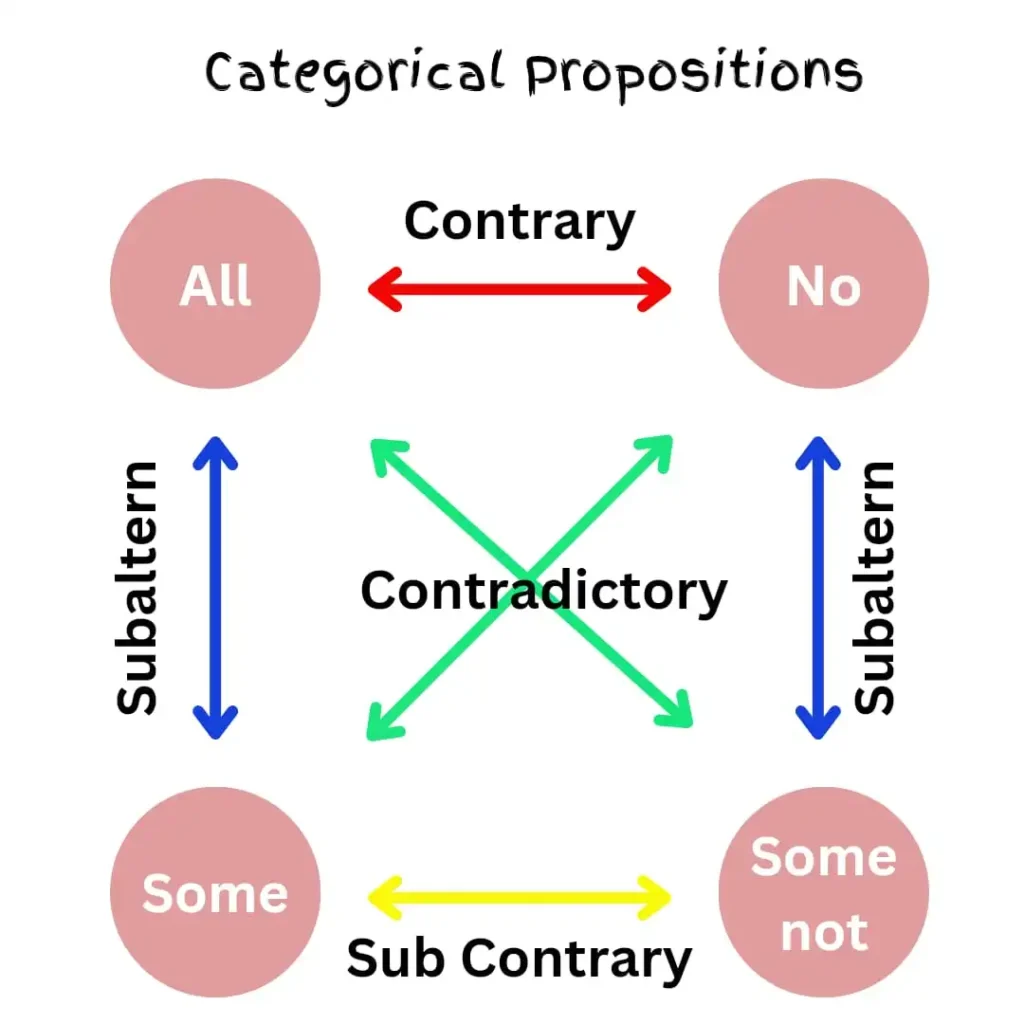
When we understand the relationships and implications illustrated by the square of opposition, we can better analyze and evaluate logical arguments, ensuring their consistency and validity.
| Relationship | Pairs | Both True | Both False |
|---|---|---|---|
| Contrary | A and E | No | Yes |
| Sub contrary | I and O | Yes | No |
| Subalton | A and I and E and O | Yes | Yes |
| Contradictory | A and O and E and I | No | No |
Conclusion
To sum up, developing good logical reasoning abilities requires an in-depth knowledge of categorical proposition principles. They are four different types of categorical propositions, the distributed and undistributed nature of statements, and the square of opposition.
We can improve our capacity for critical thought and produce more reliable decisions by incorporating these ideas into our arguments and reasoning processes. So take advantage of the strength of categorical assertions and push the boundaries of your logical thinking.
It’s your turn now to go further into the realm of categorical propositions and expand your knowledge of logic. See the improvement in your decision-making processes when you begin applying these ideas to your regular reasoning.
For free mock test




